Research into integer sequences at WIT

2005

YEAR BOOK

Home Page	Table of contents	Index by Author	Index by topics
Search

Waterford Institute of Technology

Paul Barry

Research into integer sequences at WIT

One of the most fundamental building blocks of mathematics is the humble number. Since antiquity, numbers, and in particular, whole numbers, have exercised the minds of many learned people. With time, mathematics has moved on, and discovered far more complex entities, which require deeper tools of analysis. Despite this, the investigation of whole numbers, and in particular sequences of such numbers, remains a very active area of research. For instance, it is just over ten years ago since one of mathematic's most famous puzzles regarding whole numbers was solved. This was the famous "Fermat's last theorem", which can be stated in a manner that anybody familiar with Pythagoras' theorem could understand, and which defeated some of the best mathematical minds for over 350 years. More recently, in 2004, a particularly historic event in the study of number sequences took place. This was the entry of the 100,000-th sequence into the On-line Encyclopedia of Integer Sequences, an electronic store house of sequences of integers that contains some of the most important sets of numbers used in mathematics, physics and other areas of science. This is maintained by Neil Sloane of the ATT labs in New Jersey. It can be accessed at http://www.research.att.com/~njas/sequences .

The best known example of a whole number sequence is of course the counting numbers, 1,2,3,.... Probably the best known 'non-trivial' integer sequence (an integer is a whole number that can be positive, negative or zero) is the sequence of Fibonacci numbers, 0,1,1,2,3,5,8,.... where each number is the sum of the last two numbers. In modern times, this sequence has gained a world-wide readership, as it is featured in the best-selling thriller "The Da Vinci Code", by Dan Brown. These numbers do indeed have many interesting features, and an analysis of many naturally occurring objects can motivate their study. From these numbers comes the idea of a "Divine Proportion", which has been used by artists and architects since antiquity, including Leonardo Da Vinci himself. This sequence has defining equation f(n)=f(n-1)+f(n-2). A variant studied in more recent times, the Padovan sequence 1,1,1,2,2,3,�, is given by the simple generalization f(n)=f(n-2)+f(n-3). This sequence also gives rise to interesting architectural proportions, a fact that has led to its use by some modern designers of buildings.

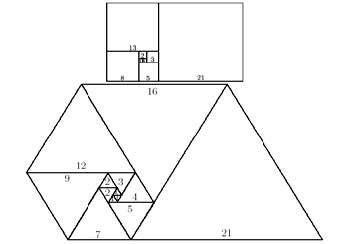
Figure 1 Fibonacci and Padovan proportions

The even simpler variation f(n)=f(n-1)+2*f(n-2) on the Fibonacci numbers leads to the Jacobsthal numbers, which, for instance, are related to the number of ways that a person could start walking from a vertex of a triangle, and return to it, going through as many of the vertices as many times as they liked. It can also be shown that these numbers, which begin 0,1,1,3,5,11,21,.. count the number of ways that it is possible to knot a tie � there being up to 85 ways, in practice.

Computer scientists will be familiar with the set of numbers 1,3,7,15,31,... which has the formula 2^n-1. These are sometimes called the Mersenne numbers, and are intimately linked to the Towers of Hanoi problem. This puzzle was invented by the French mathematician Edouard Lucas, who was the first to popularise the Fibonacci numbers.

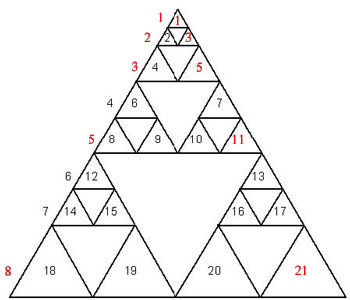
Figure 2 Jacobsthal and Fibonacci numbers in a Sierpinski-like triangle

From a mathematical point of view, the most versatile integer sequence is probably the set of Catalan numbers. The first few are 1,1,2,5,14,42,.... but their definition is less elementary than the sequences above. The list of things that they count continues to grow. For instance, they count the number of triangulations of regular polygons, the number of lattice paths from (0,0) to (n,n) using only horizontal and vertical steps of length one, which do not go below the diagonal line y=x, the number of binary bracketings of n letters, and many other objects.

A mathematical object that links all these sequences and which all secondary school students are familiar with is Pascal's triangle. This is the two-dimensional array of numbers that has the form

Each inner number, for instance 15, is the sum of the two numbers above it: 15=5+10. Using this rule, and always beginning and ending a row with 1, we can grow an infinite triangle. The elements of this triangle are often designated by C(n,k) where n gives the row, and k gives the column. C(n,k) in fact is the number of ways of choosing k objects from n objects. Note that the entries in the rows sum to 1,2,4,8,16,32,..... Subtracting 1 from each number, we get the Mersenne numbers. Arranging the elements of Pascal's triangle as

and adding all shallow diagonals in a west to north-east direction, we get 1,1, 1+1=2, 1+2=3, 1+3+1=5, 1+4+3=8,.... That is, we get the Fibonacci numbers 1,1,2,3,5,8,.... Now add weights 1,2,4,8,... to successive columns and repeat the process, using these weights as multipliers. We get 1*1=1, 1*1=1, 1*1+2*2=5, 1*1+3*2+1*4=11, 1*1+4*2+3*4=21,.... That is, we find the Jacobsthal numbers.

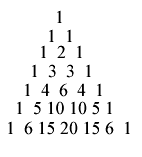
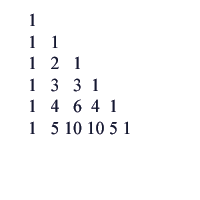
To find the Catalan numbers, we look at the central column of numbers 1,2,6,20,... These are called the central binomial numbers, and are very important in their own right. Dividing this sequence by the sequence 1,2,3,4,... we get 1/1=1, 2/2=1, 6/3=2, 20/4=5, .... That is, we get the Catalan numbers 1,1,2,5,14,... Their formula is then C(2n,n)/(n+1).

The branch of mathematics that studies these entities is called combinatorics, as it involves the counting of objects in different combinations.

Many properties of sequences can be elucidated by finding transformations that map one sequence into another. We can then study the transformation, rather than a particular sequence, and derive results about whole families of sequences. Some of the most important transformations are members of the "Riordan group". This is made up of infinite matrices of a form known as 'lower-triangular' which have ones down the main diagonal, and which have a special algebraic representation. The second representation of Pascal's triangle above is an example of such a matrix. As an element of the Riordan group, it has the simple algebraic representation (1/(1-x), x/(1-x)). Applying this particular transformation to a sequence is known as taking the binomial transform of the sequence. For instance, the binomial transform of the sequence 1,2,4,8,16,... with general term 2^n turns out to be the sequence 1,3,9,27,81,... with general term 3^n. This fact was first recorded in 1227. This is in fact a simple consequence of the well-known Binomial Theorem.

A less elementary transformation is given by (1, c(x)), where c(x) has the form (1-sqrt(1-4x))/(2x). c(x) is a function which 'generates' the Catalan sequence. This transformation maps the constant sequence 1,1,1,...., to the Catalan sequence. An interesting feature of these transformations is that they have inverses. For instance, the inverse of the binomial transformation has algebraic from (1/(1+x), x/(1+x)). In terms of numbers, its matrix begins

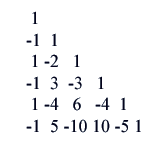
As an example, it transforms the constant sequence 1,1,1,... to the sequence 1,0,0,....

The inverse of the "Catalan" transform (1, c(x)) has the simple form (1, x(1-x)). Interestingly, this has a matrix representation that is a rotated version of the inverse binomial transformation:

The general term of this matrix is given by (-1)^(n-k)*C(k,n-k). If we sum the absolute values of the row elements of this matrix, we get the Fibonacci numbers once more. That is, the Fibonacci numbers are obtained by summing C(k,n-k) over k. Similarly, the Padovan numbers can be obtained by summing C(k,n-2k) over k.

Figure 3 A Jacobsthal-Sierpinski triangle

Sloane's On-line Encyclopedia of Integer Sequences currently contains almost 110,000 entries and it grows by over 10,000 sequences a year. It is the result of a collaborative effort by mathematicians over a 40 year period, and continues to grow. Readers are invited to visit it at the web address given above, to check on the details of their favourite sequences or to add their favourite sequence, if it is not already there.

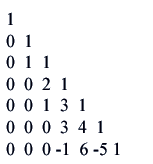
Contact: Paul Barry, School of Science, WIT;
E-mail [email protected]