2006 IRISH SCIENTIST YEAR BOOK

Home Page

Table of contents

Index by Author

Index by topics

Search


University of Limerick
Clifford Nolan, Romina Gaburro, Thomas Dowling & Niall Ryan
Inverse problems: the mathematics behind imaging

Imaging science has an increasing impact on our daily lives. For example, the image obtained from an ultrasound scan of a baby in a mother's womb is the result of data collection and mathematical analysis. The aim is to reconstruct as faithfully as possible the form of the developing baby. Another important example of imaging is the testing of computer components and aircraft for flaws and cracks.


The current methods underpinning such scans are often surprisingly unsophisticated! For example, a basic ultrasound image is obtained by simply plotting the intensity of reflected sound waves i.e., echoes, directly on a screen at a position calculated by a simple 'time of flight to depth' conversion. In other words, if we measure how long the echo takes to come back, we can calculate the depth to the point in the womb where the wave reflected. To get that depth, we simply divide the echo time by the speed of sound (in water, since we are composed mostly of water!).

Our research at the University of Limerick is funded by Science Foundation Ireland. We are developing a radically new methodology leading to faster and improved imaging techniques. Our methods not only give a qualitative impression of the internal structure of materials but also give quantitative information about the material properties, such as density and electrical parameters. The applications include medical imaging, non-destructive testing of materials, navigational systems, etc.

The generic imaging technique we propose uses various types of waves (such as ultrasound, X-ray and other radio waves, elastic waves, etc) to probe the internal structure of an object. From measurements of the reflected waves, we are able to process this information and display an image of the internal structure of an object. This is accomplished in a non-invasive/destructive manner.

When an ultrasound pressure wave impinges on the interface between two different kinds of materials with different densities (e.g. healthy tissue surrounding a denser tumour), it will reflect at the interface. The reflected pressure waves are measured and can be mathematically expressed as an integral over the interface of the difference of densities:


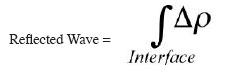
i.e., a surface integral, or 'integral transform' of the density differential. This draws on a whole field of mathematics called 'integral geometry', which studies integrals of functions over surfaces. The goal is to 'invert' the integral transform and obtain the density differences on the interface from the measured reflected waves. This is an example of solving an 'inverse problem' in mathematics.

We are able to marry various mathematical tools such as inverse problems, integral geometry, geometrical optics, partial differential equations, Fourier and harmonic analysis, algebraic and differential geometry to accomplish the latter task. The breadth and abstractness of the mathematical tools employed is astonishing when one considers how we are using these tools in such an applied and practical field as imaging.

To conclude, our method applies another integral transform to the reflected pressure wave measurements to obtain the required image. The asymptotic theory of geometrical optics is incorporated in this transform and lends itself well to obtaining images very rapidly indeed. This is a major strength of our method.

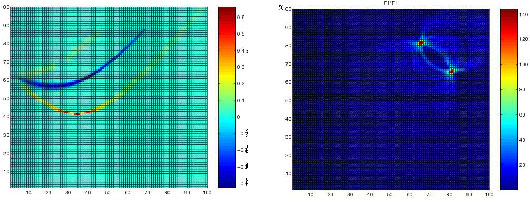
The included figures depict RADAR data (the reflected waves appearing as hyperbolic curves) and the reconstructed image of the reflecting structure.

Our project takes place in the broader context of the Network for the Application of Mathematics to Science and Industry. This is a Science Foundation Ireland funded project based at the University of Limerick. The focus of the project is mathematical modelling of processes arising in science and industry. The combined funds for both projects are approximately five million euro over the next five years.

If you would like more information on our imaging work, please contact Clifford Nolan via e-mail ( [email protected] ).
For more information on research in the wider context of our department, please contact Stephen O' Brien ( [email protected] ).
And of course, you can always visit the mathematics department web page at www.maths.ul.ie