| 2006 |

|
YEAR BOOK |
Dublin Institute for Advanced Studies
|
Looking beyond the Silicon Age
|
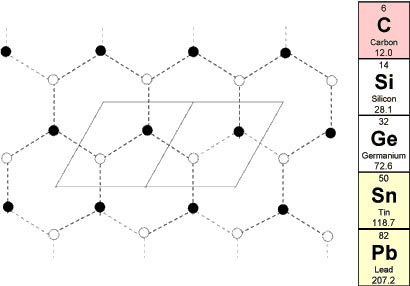
In 2004, an important advance happened in Manchester and Chernogolovka. Carbon makes diamonds, but what causes a deeper glitter in some eyes is graphite. This is a stack of sheets, each one formed by a honeycomb of carbon atoms. Single sheets can be peeled off and got a name of their own, graphene. Tubes make the famous carbon nanotubes, but sheets are easier to standardise and have much less problems with external contacts. Electron mobility is not quite as high as in the tubes, but still twenty times higher than in silicon, so one certainly can build ultrafast transistors. Eventually, one will be able to shoot the electrons directly at their targets, without much dissipation. Then quantum mechanics will show its full power.
The quantum properties of graphene involve not only Schr�dinger's quantum mechanics, but even relativistic quantum field theory ( E=mc 2 and all that), though electrons in ordinary matter cannot approach the speed of light. In graphene, however, the electric interactions conspire to simulate a two-dimensional relativistic quantum field theory, just with a much smaller maximal velocity. One can glimpse part of the reason by subdividing the honeycomb lattice into identical tiles. Each such tile must contain exactly two carbon atoms [see the figure], which yield two highly mobile electrons. When one looks at the global behaviour of graphene, these two states conspire to form a two-dimensional analogue of electron spin.
As a consequence, graphene shows a very strange quantum Hall effect. Recall that this effect concerns magnetic fields and their perpendicular force on electric currents. In Hall's time, this concerned diffusing electrons. About a hundred years later a dissipationless quantum Hall effect was discovered in sheets of gallium arsenide in a strong magnetic field and with a voltage across the sheet. One obtains perpendicular currents with a conductivity unit of e 2 /h = 1/(25,812.8075 ohm), where e is the electron charge and h is Planck's constant. A nice mathematical proof shows that the conductivity can be 0 or e 2 /h but nothing in between: The states of the electrons fill out a closed surface in some abstract space. When one puts it around a sphere it either can be unwrapped completely or not at all. This always works when the number of electrons is finite, which is of course true in every lab. For quantum field theories this argument breaks down, however. Due to the creation of particles and anti-particles even the vacuum contains a sea of infinitely many electrons and instead of a sphere one has an infinite cone. When one calculates the corresponding Hall conductivity, one finds just one half of e 2 /h . Indeed this was found in recent graphene experiments at Columbia University ( Nature 438, November 2005). The nice mathematical proof applies in a new way, since in graphene the cones do not really extend to infinity. The two states mentioned above yield two long cones, which eventually join to form a sphere.
Nevertheless, the electrons behave relativistically, and technology could make good use of this property. In particular, one might cut graphene sheets and use dissipationless currents along their edges. With suitable magnetic modifications of the material, these currents could be given a preferred direction, and calculations show that a very fine control is possible. At present, this is merely the abstract mathematics of quantum mechanics, but it may be worth a very careful look. Magnetically active modifications of graphite are under active study in Ireland ( Physics World , November 2004). What is lacking most is expertise in low temperature physics, where dissipationless motion is easier to achieve. Perhaps the future leaders of SFI will do something about it.
Contact: Professor Werner Nahm and Dr. Marianne Leitner
School of Theoretical Physics
Dublin Institute for Advanced Studies
10 Burlington Road, Dublin 4;
Tel. (01) 6140143
E-mail: [email protected]