2006 IRISH SCIENTIST YEAR BOOK

Home Page

Table of contents

Index by Author

Index by topics

Search


Synge Street CBS, Dublin
Keith Florea, Adrian Chisa & Sandeep Sihag
A hodograph is the curve traced out by the tips of the velocity vectors of a moving body when these vectors are all translated to a common origin.


Adrian Chisa, Keith Florea and Sandeep Sihag (centre) at the exhibition with one of their teachers, Ms Stephanie Maher, and two schoolfriends.

The hodograph was invented by William Rowan Hamilton in a paper he wrote in 1847. In this paper he proved that for the Kepler problem, that is, the motion of a body attracted to a fixed point by an inverse square force law, the hodograph is a circle irrespective of the shape of the orbit (ellipse, parabola, hyperbola).

Hamilton's hodograph theorem follows from the fact that there is a vector � which we call the "Hamilton vector" � that remains constant throughout the motion.

Other mathematical physicists of Hamilton's era and just after it mentioned the hodograph in their writing, but in the twentieth century this concept was rarely mentioned in physics books.

For anyone who is learning computer simulation techniques in physics, the motion of planets and satellites is a very attractive application of simulation methods. The issue of the accuracy of a particular simulation technique is always of central importance. In our project we use the hodograph of the motion and the constancy of the Hamilton vector to test the accuracy of a number of simulation techniques for the Kepler problem. We have developed three estimators of the simulation error based on the use of hodographs. The methods we describe are a fresh approach to checking the accuracy of such simulations.


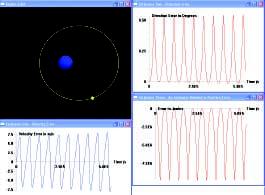
Screenshot showing the time variation of the error estimators

We programmed our simulations in Python. Python is a powerful computer programming language developed during the 1990s. VPython is a 3D graphics extension to Python specifically designed with physics simulations in mind. Vectors are a fundamental data-type in Python. Using Python/VPython it is possible to write very concise, easily understood 3D physics simulation programs.

The goals of our project are:

� to provide a new simple technique for people wishing to evaluate the accuracy of various simulation methods in the Kepler problem,
� to highlight Hamilton's invention of the hodograph and his theorem that the hodograph of the Kepler problem is always a circle,
� to point out the importance and usefulness of the Hamilton vector,
� to highlight the work of Feynman and others on the derivation of the properties of Keplerian orbits from the hodograph.
Keith, Adrian and Sandeep entered their project in the Senior Group Section in the Chemical, Physical & Mathematical Sciences Category at the BT Young Scientist & Technology Exhibition and won The Best Group Award. Their teacher was Mr Jim Cooke.

This article was sponsored by Oldbury Publishing Limited.